힙 정렬 (Heap Sort)

Posted Nov 9, 2023

By 21 min read

힙정렬 (Heap Sort)

힙(HEAP) 정렬의 역사
개발 배경
힙(HEAP) 정렬의 기본 개념
최대 힙(Max Heap) 정렬 과정 요약
최소 힙(Min Heap), 최대 힙(Max Heap), 일반 이진 트리 (Binary Tree)
비-리프 노드(Non-leaf Node)와 리프 노드(Leaf Node)
힙(Heap) 정렬 알고리즘 예시 [최대 힙 구축]
최대힙 구축 알고리즘
최대힙 구축 후 정렬 알고리즘
최종 알고리즘
정렬 알고리즘의 특성 비교

힙(HEAP) 정렬의 역사

J. W. J. Williams에 의해 1964년에 처음으로 개발된 힙 정렬은, 영국 출신의 수학자이자 프로그래머인 Williams에 의해 개발되었습니다. 그는 런던 대학교 킹스 칼리지에서 수학 학사 학위를 받은 후 캐나다로 이주하여 통신 분야에서 연구와 개발 활동을 펼쳤습니다.

개발 배경

효율성 향상: Williams는 기존의 정렬 알고리즘들이 큰 데이터 세트에 대해 비효율적이거나 시간이 많이 걸린다는 점에 주목했습니다. 힙 정렬은 O(n log n)의 시간 복잡도를 가지며, 이는 평균적이고 최악의 경우에서도 우수한 성능을 제공합니다.
메모리 최적화: 초기 컴퓨터 시스템은 메모리 리소스가 제한적이었습니다. 힙 정렬은 추가적인 메모리 할당 없이 정렬을 수행할 수 있는 in-place 알고리즘으로, 메모리 효율성을 높일 필요가 있었습니다.
범용성과 실용성: Williams는 다양한 유형의 데이터와 다양한 컴퓨팅 환경에서 적용할 수 있는 범용적이고 실용적인 정렬 방법을 개발하고자 했습니다.

논문: Williams, J. W. J. (1964), “Algorithm 232 - Heapsort”, 《Communications of the ACM》 7 (6): 347–348, doi:10.1145/512274.512284

힙(HEAP) 정렬의 기본 개념

힙의 정의: 힙은 완전 이진 트리로서, 각 노드의 값이 자식 노드의 값보다 크거나(최대 힙) 작거나(최소 힙) 하는 조건을 만족합니다. 힙 구축: 정렬할 배열을 최대 힙 또는 최소 힙으로 구성합니다. 이 과정에서 모든 Non-leaf Node 에 대해 하향식 힙 조정(heapify) 작업을 수행합니다. 최대 힙을 사용하면 배열의 가장 큰 요소가 힙의 루트에 위치하게 됩니다.

최대 힙(Max Heap) 정렬 과정 요약

n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부모노드, 왼쪽 자식노드, 오른쪽 자식노드 순으로 구성한다.
최대 힙을 구성한다. 최대 힙이란 부모노드가 자식노드보다 큰 트리를 말하는데, 단말 노드를 자식노드로 가진 부모노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.
가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.
2와 3을 반복한다.

최소 힙(Min Heap), 최대 힙(Max Heap), 일반 이진 트리 (Binary Tree)

특성	최소 힙(Min Heap)	최대 힙(Max Heap)	이진 트리(Binary Tree)
정의	각 부모 노드의 값이 자식 노드의 값보다 작거나 같음	각 부모 노드의 값이 자식 노드의 값보다 크거나 같음	부모-자식 관계를 가진 노드들의 계층적 구조
특징	힙 내에서 가장 작은 값이 루트에 위치	힙 내에서 가장 큰 값이 루트에 위치	특정한 순서 규칙이 없음
구조	완전 이진 트리 구조	완전 이진 트리 구조	이진 트리 구조 (완전할 필요 없음)
삽입/삭제 복잡도	O(log n)	O(log n)	평균 O(log n), 최악의 경우 O(n)
사용 목적	최솟값에 빠르게 접근, 우선순위 큐 구현 등	최댓값에 빠르게 접근, 힙 정렬 구현 등	데이터 저장, 검색, 이진 검색 트리 등
순서 유지	순서 유지되지 않음	순서 유지되지 않음	순서 유지될 수 있음 (이진 검색 트리의 경우)

비-리프 노드(Non-leaf Node)와 리프 노드(Leaf Node)

특성	비-리프 노드(Non-leaf Node)	리프 노드(Leaf Node)
자식 노드	하나 이상의 자식 노드를 가짐	자식 노드가 없음
트리 내 위치	트리의 루트 또는 중간 계층에 위치	트리의 가장 바깥쪽, 말단에 위치
역할	트리 구조의 지지와 데이터 전달 역할	트리의 데이터 저장의 최종 지점
예시	이진 트리에서 부모 노드로써 자식 노드를 가지는 노드	이진 트리에서 자식이 없는 마지막 노드
특징	트리의 동적 조작(삽입, 삭제 등)에 중요한 역할 수행	트리의 구조 및 크기 변경에 직접적인 영향을 미치지 않음

힙(Heap) 정렬 알고리즘 예시 [최대 힙 구축]

힙 정렬 과정은 크게 두 단계로 나뉩니다: 힙 구축 단계와 정렬 단계

1. 최대 힙 구축 단계 (Build Heap Phase)

이 단계에서는 주어진 배열을 힙 구조로 변환합니다. 최대 힙을 구축하기 위해 각 Non-leaf Node 에 대해 하향식 힙 조정(heapify) 과정을 수행합니다.

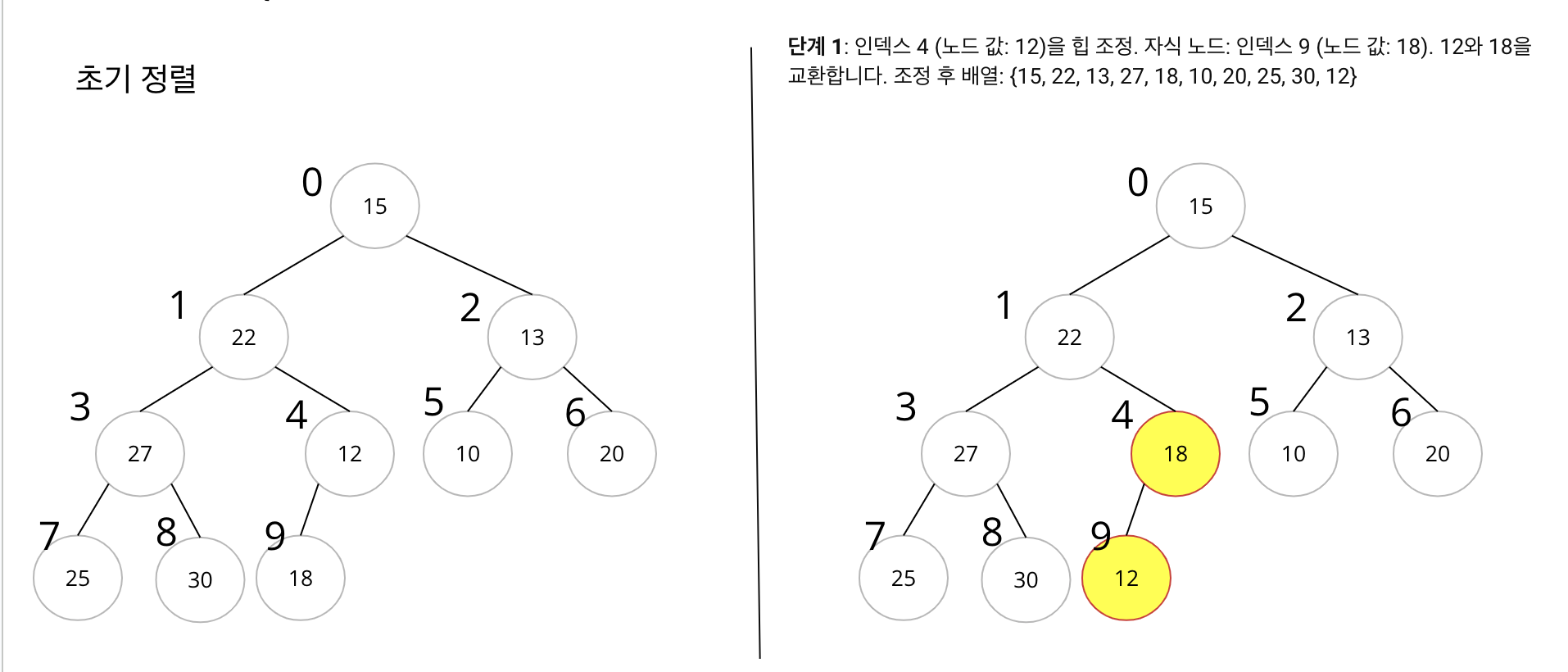
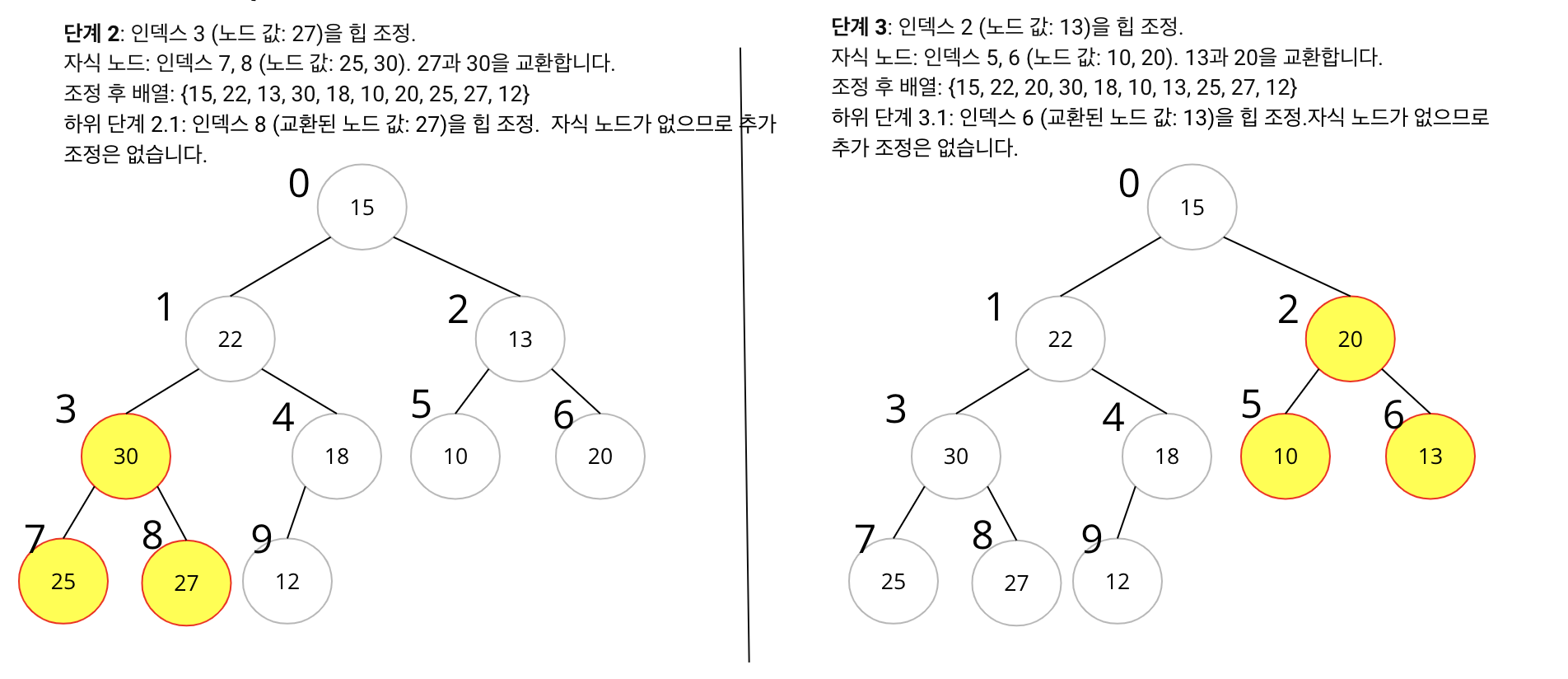
초기 배열: {15, 22, 13, 27, 12, 10, 20, 25, 30, 18}
힙 구축 과정:
- Non-leaf Node 부터 힙 조정을 시작합니다. 배열의 중간부터 시작하면 됩니다.
- 배열의 중간 인덱스는 배열 길이의 절반보다 하나 작은 위치입니다. 이 경우, 배열 길이가 10이므로, 중간 인덱스는 4입니다 (0부터 시작하는 인덱스 기준).
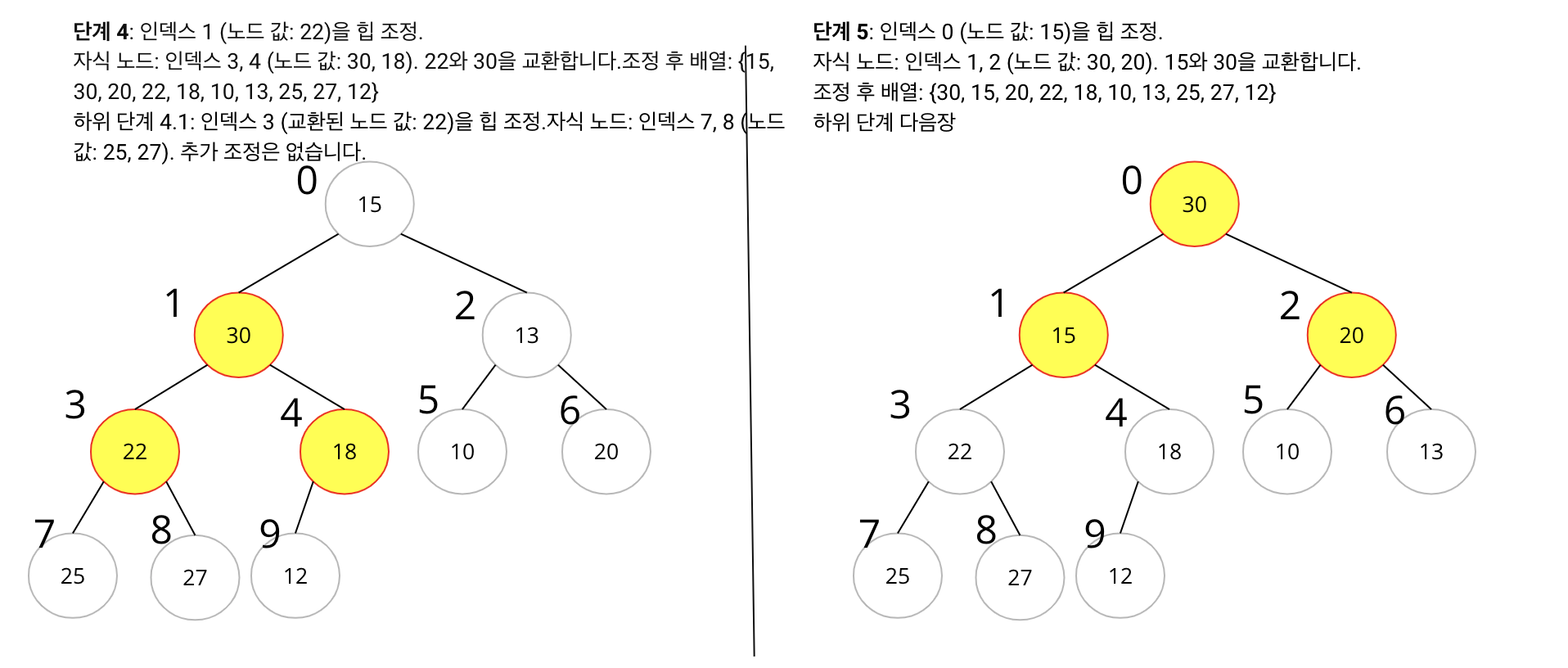
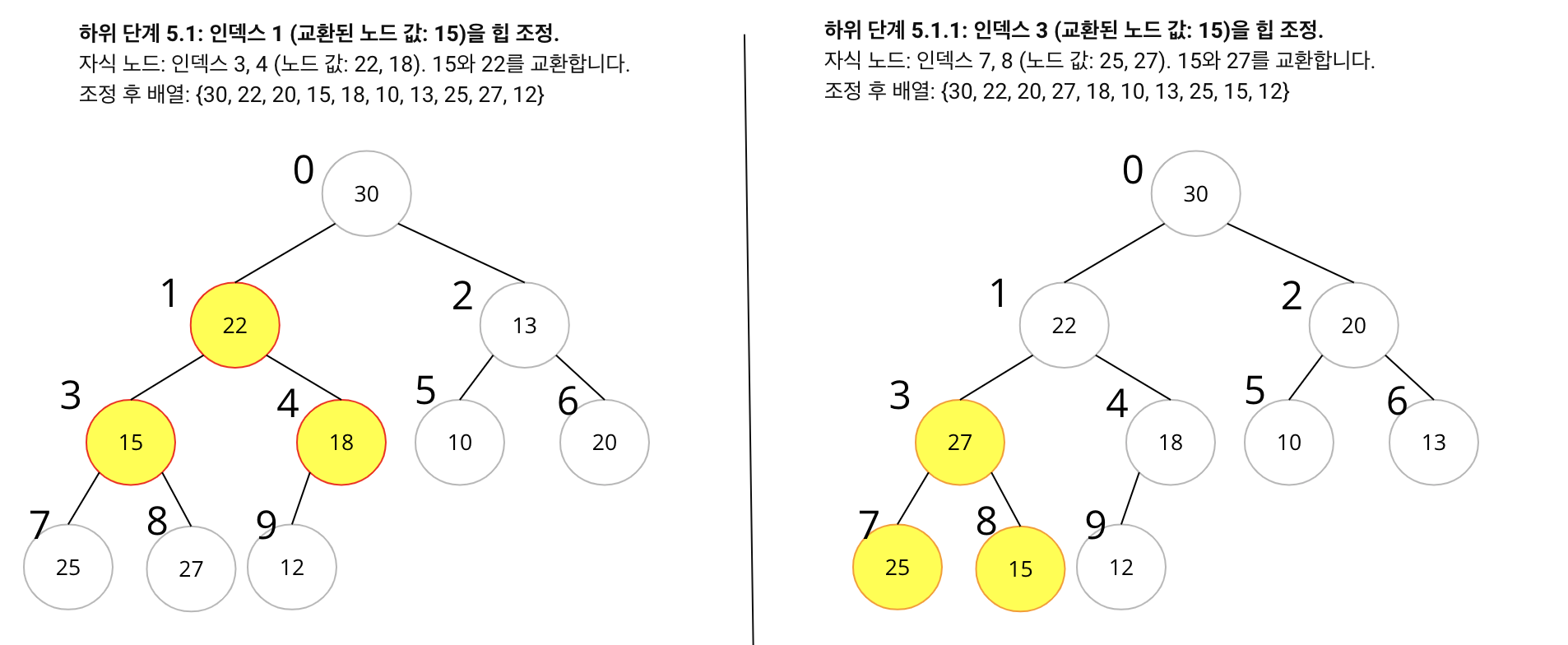
- 인덱스 4부터 하향식으로 힙 조정을 합니다.
- 각 노드에 대해, 그 노드가 자식 노드들보다 크도록 조정합니다. 만약 자식 노드 중 하나가 더 크다면, 그 자식 노드와 위치를 바꿉니다.
- 이 과정을 루트 노드에 도달할 때까지 반복합니다.

최대힙 구축 알고리즘

  
def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    # 왼쪽 자식 노드가 현재 요소보다 큰 경우
    if left < n and arr[largest] < arr[left]:
        largest = left

    # 오른쪽 자식 노드가 현재 요소보다 큰 경우
    if right < n and arr[largest] < arr[right]:
        largest = right

    # 교환 필요한 경우
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        # 재귀적으로 하위 트리 구조 조정
        heapify(arr, n, largest)

def build_max_heap(arr):
    n = len(arr)

    # 마지막 비-잎 노드부터 시작하여 첫 번째 노드까지 반복
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

# 주어진 배열
arr = [15, 22, 13, 27, 12, 10, 20, 25, 30, 18]

# 최대 힙 구축
build_max_heap(arr)
print("최종 최대 힙 배열:", arr)

Python 알고리즘: Heapify와 Build Max Heap

Heapify 함수

목적: 주어진 서브트리의 루트 노드에서 힙 속성을 복원하는 데 사용됩니다.
시간 복잡도: 최악의 경우에 트리의 높이에 비례하는 시간이 소요됩니다. 힙의 높이는 log n이므로, heapify 함수의 시간 복잡도는 O(log n)입니다.

Build Max Heap 함수

목적: 주어진 배열을 최대 힙으로 변환합니다.
작동 방식:
- 배열의 마지막 비-잎 노드부터 시작하여 첫 번째 노드까지 heapify를 호출합니다.
- 배열의 크기가 n일 때, 배열의 절반 이상은 잎 노드이므로, heapify는 약 n/2개의 노드에 대해 호출됩니다.
시간 복잡도:
- 각 heapify 호출은 O(log n)의 시간이 걸리므로, build_max_heap 함수의 총 시간 복잡도는 O(n log n)으로 계산될 수 있습니다.
- 그러나, 실제로는 트리의 높이가 감소함에 따라 heapify가 호출되는 노드 수도 감소하기 때문에, 정확한 계산은 O(n)입니다.

2. 정렬 단계 (Sorting Phase)

힙 구축 결과: 힙이 구축되면, 배열은 최대 힙의 형태를 가집니다.
정렬 방법: 힙 정렬은 최대 힙의 특성을 이용하여 배열을 정렬합니다.

정렬 과정

배열의 첫 번째 요소(최대 힙의 루트 노드, 즉 최대값)와 마지막 요소를 교환합니다.
힙의 크기를 하나 줄여 마지막 요소를 정렬된 부분으로 분리합니다.
새로운 루트(교환된 요소)에 대해 힙 속성을 복원하기 위해 heapify 함수를 호출합니다. 이 과정에서 트리의 부모-자식 간의 순서를 재조정하여 최대 힙 속성을 유지합니다.
위 과정을 배열의 모든 요소에 대해 반복합니다.

힙 정렬 과정

초기 최대 힙 배열

{30, 22, 20, 27, 18, 10, 13, 25, 15, 12}

단계별 정렬 과정

단계 1

교환 전: {30, 22, 20, 27, 18, 10, 13, 25, 15, 12}
교환 후: {12, 22, 20, 27, 18, 10, 13, 25, 15, 30}
heapify 후: {27, 22, 20, 25, 18, 10, 13, 12, 15, 30}

단계 2

교환 전: {27, 22, 20, 25, 18, 10, 13, 12, 15, 30}
교환 후: {15, 22, 20, 25, 18, 10, 13, 12, 27, 30}
heapify 후: {25, 22, 20, 12, 18, 10, 13, 15, 27, 30}

단계 3

교환 전: {25, 22, 20, 12, 18, 10, 13, 15, 27, 30}
교환 후: {15, 22, 20, 12, 18, 10, 13, 25, 27, 30}
heapify 후: {22, 18, 20, 12, 15, 10, 13, 25, 27, 30}

단계 4

교환 전: {22, 18, 20, 12, 15, 10, 13, 25, 27, 30}
교환 후: {13, 18, 20, 12, 15, 10, 22, 25, 27, 30}
heapify 후: {20, 18, 13, 12, 15, 10, 22, 25, 27, 30}

단계 5 이후

위와 같은 방식으로 계속해서 교환 및 heapify를 반복하여 배열을 정렬합니다.

최종 정렬된 배열

{10, 12, 13, 15, 18, 20, 22, 25, 27, 30}

Heapify 함수의 역할

Heapify 함수는 주어진 배열 내 특정 노드를 기준으로 하위 트리를 힙의 조건에 맞게 재구성하는 역할을 합니다.

최대 힙에서의 Heapify 과정

노드 선택

배열 내 특정 인덱스에 위치한 노드를 기준으로 시작합니다.

자식 노드 확인

해당 노드의 왼쪽 및 오른쪽 자식 노드를 확인합니다.

최대 값 찾기

선택된 노드와 두 자식 노드 중에서 가장 큰 값을 찾습니다.

조건 비교 및 교환

만약 선택된 노드가 가장 크지 않다면, 가장 큰 자식 노드와 해당 노드를 교환합니다.
이렇게 함으로써, 부모 노드는 언제나 자식 노드보다 크거나 같은 성질을 유지합니다.

재귀적 처리

교환된 자식 노드에 대해서도 동일한 heapify 과정을 재귀적으로 적용합니다.
이는 교환된 자식 노드의 하위 트리가 힙의 조건을 만족하도록 보장합니다.

최대힙 구축 후 정렬 알고리즘

  
def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    # 왼쪽 자식이 현재 요소보다 크면
    if left < n and arr[i] < arr[left]:
        largest = left

    # 오른쪽 자식이 현재 요소보다 크면
    if right < n and arr[largest] < arr[right]:
        largest = right

    # 최대값이 현재 노드가 아니면
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # swap
        heapify(arr, n, largest)

def heapSortWithoutBuildingHeap(arr):
    n = len(arr)

    # 하나씩 추출하면서 정렬
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # swap
        heapify(arr, i, 0)

# 입력값이 이미 최대 힙인 배열
arr = [30, 27, 25, 22, 20, 18, 15, 13, 12, 10]
heapSortWithoutBuildingHeap(arr)

Heapify 함수

Heapify 함수는 주어진 서브트리의 루트 노드에서 힙 속성을 복원하는 데 사용됩니다. 이 함수는 최악의 경우에 트리의 높이에 비례하는 시간이 소요됩니다. 힙의 높이는 log n이므로, heapify 함수의 시간 복잡도는 O(log n)입니다.

HeapSortWithoutBuildingHeap 함수

이 함수는 배열의 각 요소에 대해 heapify를 호출합니다. 배열의 각 요소에 대해 heapify를 한 번씩 호출하므로, 총 n번의 호출이 이루어집니다. 각 heapify 호출은 O(log n)의 시간이 걸리므로, 전체 heapSortWithoutBuildingHeap 함수의 시간 복잡도는 O(n log n)입니다.

최종 알고리즘

  
 def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[largest] < arr[left]:
        largest = left

    if right < n and arr[largest] < arr[right]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def build_max_heap(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

def heap_sort(arr):
    n = len(arr)
    build_max_heap(arr)

    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, i, 0)

# 주어진 배열
arr = [15, 22, 13, 27, 12, 10, 20, 25, 30, 18]

# 힙 정렬 실행
heap_sort(arr)
print("정렬된 배열:", arr)

정렬 알고리즘의 특성 비교

정렬 알고리즘	평균 시간 복잡도	최악의 시간 복잡도	공간 복잡도	안정성	사용처	장단점
버블 정렬 (Bubble Sort)	O(n²)	O(n²)	O(1)	안정	작은 데이터셋, 교육용	간단하고 이해하기 쉬움, 매우 비효율적
선택 정렬 (Selection Sort)	O(n²)	O(n²)	O(1)	불안정	작은 데이터셋, 메모리 제약이 심한 경우	구현이 간단, 비효율적이며 안정성이 없음
삽입 정렬 (Insertion Sort)	O(n²)	O(n²)	O(1)	안정	작은 데이터셋, 거의 정렬된 데이터	간단하고 효율적, 최악의 경우 비효율적
합병 정렬 (Merge Sort)	O(n log n)	O(n log n)	O(n)	안정	큰 데이터셋, 외부 정렬	일관된 성능, 추가 메모리 필요
퀵 정렬 (Quick Sort)	O(n log n)	O(n²)	O(log n) (평균)	불안정	큰 데이터셋, 평균적으로 빠름	매우 빠름, 최악의 경우 비효율적
힙 정렬 (Heap Sort)	O(n log n)	O(n log n)	O(1)	불안정	큰 데이터셋, 메모리 제약이 심한 경우	추가 메모리 필요 없음, 일관된 성능

Algorithms

algorithms

This post is licensed under CC BY 4.0 by the author.

힙정렬 (Heap Sort)

힙(HEAP) 정렬의 역사

개발 배경

힙(HEAP) 정렬의 기본 개념

최대 힙(Max Heap) 정렬 과정 요약

최소 힙(Min Heap), 최대 힙(Max Heap), 일반 이진 트리 (Binary Tree)

비-리프 노드(Non-leaf Node)와 리프 노드(Leaf Node)

힙(Heap) 정렬 알고리즘 예시 [최대 힙 구축]

1. 최대 힙 구축 단계 (Build Heap Phase)

최대힙 구축 알고리즘

Python 알고리즘: Heapify와 Build Max Heap

Heapify 함수

Build Max Heap 함수

2. 정렬 단계 (Sorting Phase)

정렬 과정

힙 정렬 과정

단계 1

단계 2

단계 3

단계 4

단계 5 이후

최종 정렬된 배열

Heapify 함수의 역할

최대 힙에서의 Heapify 과정

노드 선택

자식 노드 확인

최대 값 찾기

조건 비교 및 교환

재귀적 처리

최대힙 구축 후 정렬 알고리즘

Heapify 함수

HeapSortWithoutBuildingHeap 함수

최종 알고리즘

정렬 알고리즘의 특성 비교

Trending Tags